如何用小概率赚大钱? 12 Oct 2019, 16:35
· Views 2,959
View translation
真的有以小博大这回事吗?
有。
但并不是以下这些。
首先 ,不是买彩票;
其次 ,也不是赌博;
第三 ,更不是对消息股或比特币的All in。
那到底是什么呢?
本文将向你揭示一个秘密:
有些小概率事件可以叠加成大概率事件,而该事件因为“小概率”而拥有的特别选择权,会带来赚大钱的机遇。 一
我们先倒过来想,看一个极小概率但是亏大钱的例子。
请看题目。
幸存的青花瓷
明青花瓷非常值钱。例如,明永乐年间的青花如意垂肩折枝花果纹梅瓶(高36.5 cm),2011年曾以1.6866亿港元成交。
我们假设一只青花盘在一年内被失手打破的概率是3%。
如果明朝正德年间(距今约500年)生产了一万只青花麒麟盘,请问现在还剩多少个?
(题目来自何书元编著的《概率论》)
假如不计算,你随便估一下,现存多少正德青花麒麟盘? 我在上一篇 《 为什么真正聪明的人都是概率高手?(零公式入门篇) 》 里介绍了这类问题的计算方法。 500年间不被打破的概率p=(1-0.03)的500次方=2.43乘以10的负七次方。 一万只青花盘被打破的概率是q的一万次方=0.99757 那么这一万只盘子,至今仍然幸存的概率是1-0.99757=0.00243。 也就是说,在今天,有千分之2.43的概率还能见到这种青花盘。 假如当初(明朝正德)生产了500万个青花盘,今天还会剩多少个呢?
就像上面青花盘的例子,每年打破的概率只有百分之三,而且足足有500万个,但是历经500年,也剩不下一个。 墨菲定律的原句是:如果有两种或两种以上的方式去做某件事情,而其中一种选择方式将导致灾难,则必定有人会做出这种选择。
“墨菲定律”(英文:Murphy's theorem)主要内容有四个方面:
四、如果你担心某种情况发生,那么它就更有可能发生。
墨菲定律似乎是热力学第二定律的世俗版。作为热力学的三条基本定律之一,热力学第二定律表述热力学过程的不可逆性: 孤立系统自发地朝着热力学平衡方向──最大熵状态──演化,同样地,第二类永动机永不可能实现。 500万只青花盘,在500年间不可避免地被一一摔碎,似乎在说,墨菲定律和熵增,本质上是一回事情。 用熵增来解读,盘子会从当前这个有序的状态(好盘子),到无序的状态(碎盘子)。
巴菲特说:你要买那些傻瓜也能经营好的公司,因为一切公司早晚会落到傻瓜手里。
如果从有序到无序“不可逆转”,为什么人类还能在地球上繁衍进化呢? 既然小概率事件在样本量足够大的时候无法避免,那么,我们押“青花盘早晚会碎掉”,是不是可以从中赚大钱呢? 最生动的案例莫过于电影《大空头》里所讲述的真实故事。
片中蝙蝠侠扮演的是一位投资界的传奇人物迈克尔·伯里 ,他于2000年成立 Scion 基金,至2008年, 基 金投资人实现的扣除费用后净回报率是489%。 迈克尔·伯里 小时候失去一只眼睛,性格孤僻,也许因此而更善于独立思考。他本职是医生,起初是个业余投资者。1、起初他是格雷厄姆的“价值投资”信徒,后来也许仍然是,只不过运用得更加自由奔放; 2、也许是因为起点很低,他开始在便宜、冷门、小市值、流动性差的股票里找机会; 3、他的核心策略是,在100%遵守安全边际的原则下,去寻找被严重低估的便宜货; 概括而言,他是一个对概率波动有更大承受力的价值投资者 。
大空头的攻略
时间: 2005年-2007年。
机会: 2005年,发现美国房贷还款记录糟糕,违约率不断上升。
下注: 赌地产泡沫会破裂,做空次级房贷。
赌注: CDS。若输每年缴1.5%保费,若赢赚30-50倍保费赔付。
过程: 从2005年开始下注,2006年基金大幅回撤,饱受煎熬。
结果: 2007年,次级房贷危机爆发,大赚一笔。
有一个价值两亿的明朝青花盘,被一个土豪放在家里的客厅炫耀。有次你去他家做客,发现他家有三个熊孩子,每天打打闹闹,经常打坏东西,家长呵斥也没用。 你心想,尽管主人很小心,早晚那个盘子会被熊孩子们毁掉。
所以两年内不被打碎的概率是(1-30%)✖️(1-30%)=49%;
也就是说,两年内被打碎的概率(1-49%)=51%。
于是,你对主人说:我们来合作一把,我来出钱帮你这个盘子买个保险,万一出事儿了,赔付的钱我们对半分。 大概是这个意思吧(我们先别“杠”这个假故事的合理性和细节)。 回到《大空头》,即使迈克尔·伯里 预测准了次贷危机会发生,谁会给他以小博大的筹码呢? 这个工具就是CDS(Credit Default Swap信用违约互换):相当于你给别人的房子买保险,赔钱的话算你的。 CDS被比喻为 “ 为大火正要吞没的房子投保,房子是别人家的 ”。 CDS费率每年只要1.5% , 合约的期限可以长达30年 。 用我们上面的概率计算来看,这个看起来像赌博的游戏,胜率接近100%,而爆掉的风险则很小。 你看看,这像不像一个局外人版的“俄罗斯转盘游戏”: 有一群人在玩儿俄罗斯转盘游戏,大家用装了一颗子弹的左轮手枪射自己的脑袋。 你坐在旁边,下注只要有人中弹你就能赚50万,但是你要付给每个射自己但没中弹的家伙一次一百块钱。 1、不管多么小概率,只要玩儿下去,一定会有人中弹; 问题就在于,馅饼出现的时候,极少有人认为这是个馅饼。 他阅读了上百份抵押债券说明书,每份说明书都有上百页。 据说他是除律师之外,第一个真正 仔细阅读这些复杂文件的人。 从下注到青花盘被打碎,迈克尔·伯里 等了三年。这中间因为2006年基金大幅回撤,他饱受投资人的摧残,一般人早就坚持不下去了。 即使后来证明他赌对了,投资人们也早早赎回,没让他创造出更大奇迹。 投资就是这样,馅饼即使摆在眼前,人们也未必看得清楚。 疑惑1: 慢着,我们平时不总是听说,要下注于大概率事件吗? 对于这个问题,需要从两个角度分析,才会有更直观的感知。 用一个稍微笼统的描述,就是:负期望值的事情没法叠加成正期望值的事情 。 在上面《大空头》的例子里,迈克尔·伯里 的成本即使叠加10年,对于30-50倍的预期回报,也是一件“正期望值”的事情。 而一个人花几块钱买彩票,看似成本很低,但是经年累月叠加起来,极小概率的中奖概率依然极小,算下来仍然是“负期望值”的事情。 最开始小概率的事情,随着时间的累积,变成了大概率事件,你要做的,是计算付出的时间成本到底是多少,并据此计算下注的期望值。 道理虽然简单,但是即使是专业的投资人士也经常在这里栽跟头。 我记得几年前国外有位期货高手,非常准确地预测了黄金的走势。然而在预言成真前,他自己已经爆仓了 。“市场延续非理性状态的时间,要比你挺着维持不破产状态的时间长。” 1965年,90岁却无继嗣的让娜·卡尔芒签下一份在法国常见的协议,将其 公寓低价卖给自己的律师,交易时公寓的价格等于10年的生活费。 为什么价格这么低?原来,这是一个对赌协议。律师同意支付她每个月的生活费直到其去世为止,这种协议有时称作“反向贷款”。 律师于1995年12月因 癌症早一步离开人世,享寿78岁。而其遗孀继续支付卡尔芒 生活费。 塔勒布说,他的工作就是用基础不对称结构将以下4个要素联系起来: 脆弱性等于失去的比得到的更多,等于不利因素比有利因素更多,即等于(不利的)不对称性。 反脆弱性等于得到的比失去的更多,等于有利因素比不利因素更多,即等于(有利的)不对称性。
一夫一妻制中的妻子通过嫁给会计师再与摇滚明星偷情的方式实现这一转变。
作家如果白天能从事一个与写作活动无关的闲职,那么他的作品会写得更好。
如果你的90%的资金以现金形式持有(假设你不会受通货膨胀的影响),或以所谓的“保值货币”储存起来,而剩下10%的资金则投资于风险很高或者说极高的证券,那么你的损失不可能超过10%,而你的收益是没有上限的。 反之,如果某个人将100%的资金都投入所谓的“中等”风险的证券,那么他很可能由于计算错误而承受毁灭性的风险。 因此,杠铃策略弥补了罕见事件的风险不可计量且易受错误估计影响的问题,也就是说,金融杠铃策略的最大损失是已知的。
我难以想象自己成为专业写作者的情形,尽管每次回加拿大进海关被问及职业时,我总说自己是个“Writer”(这样会省很多时间)。 回到本文的“小概率”主题,塔勒布的杠铃结构其实有点儿跑题。尽管这个结构其实是提供了一个更加普世的“反脆弱”框架。
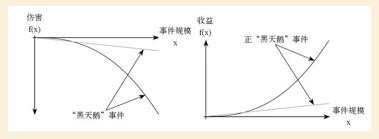
作为一位哲学家,泰勒斯面临的世俗压力有两种,一个是证明自己的智慧,一个是证明自己的“能力”。 对于哲学家来说这算不上问题,直到有一天,他听腻了生意伙伴讽刺他所说的“有能力的人从商,其他人研究哲学”的话。 我很理解泰勒斯的感触。对我这种看起来像个无用书生的人,在某些无趣的商业社交场合,有人恨不得要你把银行存款余额亮出来。 而另外一些时候,例如在我极少参加的某次公开活动中,有人质问“为什么你的公众号接了广告,你是不是很缺钱”。 假如这位质疑者知道每个月我会推掉近百个“合作广告”,以及每次广告的价格,他的“只针对他人的洁癖要求”也许会更加抓狂。 他支付了一笔首付款,以很低的租金租用了米利都和希俄斯附近的所有橄榄油压榨机的季节性使用权。 这个策略与本文前面的案例是一致的,利用了有利的不对称性。 结果是:当年橄榄大获丰收,对橄榄油压榨机的需求大幅增加,他让压榨机所有者按照他开出的条件转租机器,从中大赚一笔。 适当财富的好处是,保持思考的独立性,但又不被财富拖累(这正是斯多葛主义的关键)。 “线性”很容易理解。假如你做着一份四平八稳的工作,一个月赚一万,半年6万,一年12万,这就是线性:按比例扩大,未来是一条仿佛能望到底的直线。 第二种上凹下凸的 ,就是我们想追求的“反脆弱”的曲线。 我们总说要做时间的朋友,乍听很有道理,但是,什么是时间的朋友呢? 所谓“凸性 ”,也叫凸度 ,即convexity,是债券的一个特征。 无论何种类型的债券,都具有一定的“凸度”。凸度对于投资者而言,就是说“涨多跌少”。 凸度越大,涨的时候涨得越快;跌的时候跌得越慢。反之亦然。 开始越喝越爽,到了某个量,就达至峰值。再喝的话,就会受罪,甚至送去医院。
凸性具有反脆弱性。其可能的痛苦是有限的,而可能带来的收益则会很大。 《大空头》里做空次贷的基金经理,做多橄榄油的哲学家,都是利用上图左侧的凸性曲线。 左侧呢?喝酒,和烂人相处,赌博,为了你用不上的财富而去押上自己输不起的家底儿,都是凹性,是脆弱的。 左侧的凹性,则容易受到黑天鹅的伤害,甚至是致命打击。 在凸性的状况下,你不能犯错的时间要少得多,这仿佛某种时间的恩宠。例如Michael Burry下注之后的三年,大多时候看起来都在“犯错”,可一旦正确(大概率会发生的),仍然会实现全局性的出色业绩。
如果你拥有有利的不对称性,或正凸性(选择权是特例),从长远来看,你会做得相当不错,在不确定的情况下表现优于平均数。 不确定性越强,可选择性的作用越大,你的表现就越好。这个属性对人生来说非常重要。
在一本关于创业和风投的图书《硅谷创业课》里,反复出现了三个概念: 不是计划,不是设计,不是胸有成竹,而是模仿大自然演化过程中的混乱,捕获随机过程中新物种的涌现。 大自然懂得善于可选择性,它展示了如何以可选择性替代智慧。
这是一种与期权类似的试错机制(快速失败模型),又名 凸性自由探索 。在这一机制下,错误的成本低,最大损失是已知的,而潜在回报则是巨大的(无限)。
红杉资本的迈克尔·莫里茨说,即使是很厉害的公司,一开始有很大的不确定性,发展前景并不清晰。 “我们喜欢那些并不被大家看好的人或项目,这一直是我们做生意的方式。” 马克·安德森说,对于爱彼迎,人们惯常的想法曾经是: 所以,那些“看上去不像世界上最棒的点子”实际上更可能存在凸性,因为不确定性是明智的投资者的朋友。 如果没有一些能让初创公司的雄心壮志看起来有点疯狂的因素,项目潜在的回报不太可能是大满贯类型,而大满贯类型才是投资者获得成功的关键。 你的理论的疯狂是个不争的事实,但令我们意见不一的关键是,它是否疯狂到有正确的可能。 风险投资这门艺术的全部要点是大胆的突破性想法。大胆的突破性想法的实质是:不好预测。 霍华德·马克斯说过一句著名的话:很难进行预测,但我们可以做好准备。 具体来说,就是购买包含被错误定价的凸性机会的投资组合,而不要设法去预测不可预测的未来。 投资人认为,发现凸性的最佳地点是:其他投资人或公司创始人忽略的地方 。 然而,不管怎样,“凸性、大满贯、反向思维 ”这三个厉害的概念,还是要放进一个传统的大锅里,那就是基于概率的期望值计算。 1993年,沃伦·巴菲特致股东的信中,说明了购买包含凸性机会的投资组合这一方式:
“你可以有意识地投资包含风险的项目——有很大的可能性会带来损失或损害,但前提是:你相信概率加权后的收益将远远高于概率加权后的损失,并且你可以同时投资几个相似但不相关的项目。”
投资人霍华德·马克斯曾经对查理·芒格说过:“通过投资赚钱并不容易,任何认为此事容易的人都是愚蠢的。” 在2008年次贷危机中赚到大钱的,并非本文前面提到的独眼股神迈克尔·伯里 ,而是约翰·保尔森。
2007年,他的基金公司盈利高达150亿美元,保尔森个人收入逼近40亿美元。
2008年至2009年初,他再次为公司和客户带来了50亿美元的收益,自己也赚到了20亿美元。
2010年,保尔森以120亿美元的身价,位列福布斯全球富豪榜第45位。
2011年保尔森的基金规模达到380亿美元的高峰。
然而,随后保尔森似乎再也无法回到2007年的鼎盛时期,其平均回报回落至6.18%,其中2011年亏损9.88%。而且是在股市崛起期间。 尤其是他下大注于制药公司凡利亚,更是造成了巨大亏损。 既然投资如此不容易,我们是不是可以选择一些几乎没有风险的投资品类呢? 指数基金,似乎是巴菲特唯一向大众推荐过的投资标的。 在中国,越来越多的理性投资者不再自己选股,而是定投指数基金。 然而(没错,说起万无一失,总会有然而),我们前面的独眼股神迈克尔·伯里 又站了出来。 前不久,他认为又一个类似次贷的金融产品可能会引发崩盘。 他说的,正是指数基金 --ETF(交易型开放式指数基金)。 大量资金流入指数基金的情况正如同2008年危机前的CDO。 2004年ETF的资产规模为3380亿美元,到2018年中已高达55950亿美元,是前者的16倍。
指数基金的模型并不牢靠,被动投资者不需要做到真正的价格发现所需的安全性分析。而且流动性差,基金销售人员也在自欺欺人。 用毛姆的话来说,宇宙间的一切力量都在处心积虑要把牛奶打翻,把青花瓷打碎,把你投资账户里的钱变少。 a、假如你在两只股票里选了一只股票,你买的那只会跌,没买的那只会涨; b、忍耐是个优点,但绝等不到公鸡下蛋。你的那只重仓股就是那只公鸡; c、假如一个人对你说“这不是钱的问题”,那就一定是钱的问题; 如果从有序到无序“不可逆转”,为什么人类还能在地球上繁衍进化呢? 既然墨菲定律一直在到处捣乱,为什么还是有很多人赚到很多钱呢? 假如证券投资的赢家是随机漫步的傻瓜,那为什么还是有很多厉害的创业者呢? 一个生命有机体在不断地产生熵—或者可以说是在增加正熵—并逐渐趋近于最大熵的危险状态,即死亡。 要摆脱死亡,要活着,唯一的办法就是从环境里不断地汲取负熵……有机体就是靠负熵为生的……新陈代谢的本质就在于使有机体成功地消除了当它活着时不得不产生的全部的熵。
生命、思想以及人类奋斗的最终目的--创造能量和信息,克服熵的浪潮,并开辟有利秩序的庇护所。 让我们先看一下创业公司的“负 熵”(来自《硅谷创业课》): 1、 发现一个秘密 ,解决一个问题,传递一个核心产品价值。哪怕很毛糙,很弱小。 著名的首席执行官吉姆·巴克斯代尔总是说:“最主要的事情是保持关注最主要的事情。” 每家公司都有藏在核心价值背后的利润引擎,如果把一切无关紧要的东西去掉,这个引擎会很简单。 2、高风险、不确定性和无知的情况是不可避免的。要保持谦逊,避免过度自信。只有不断转变思想,你才能具备 从凸性中获利 的能力。 3、“要在 创始人 身上寻找的品质包括高智商、强烈的目标感、对成功的不懈追求、有进取心和竞争性、对高品质的完美主义追求、喜欢改变和颠覆、把事情做得更好的新想法、为人正直、把优秀的人聚拢在自己身边、热衷于创造真正的价值(基于洞察)。” 4、当今世界的变化无法预测,伟大的团队总是能够对这样快速变化的环境做出回应。这就是为什么投资者会花那么多钱在初创公司团队建设上。 环境变化下的“驾驭”能力比做出中期和长期规划的能力更有价值 。5、然后,追求 大满贯 的机会,并为了这个目标而 逆向思考 。 在塔勒布看来,最接近炼金术本质的,是 正收益 和 凸性效应 。
a、混为一谈问题(误将石油价格上涨归结为地缘政治,或者误将赢钱的赌博归功于良好的预测,而不是收益和可选择性的凸性效应)的严重程度。 b、为什么任何具有可选择性的事物都具有长期优势——以及如何来衡量它。
尽管我是在本文写到一半时,才不得不翻出《反脆弱》这本已经算不上时髦的书(一方面是因为那些最基本最重要的道理大多一样,一方面是因为聪明的作者实在不多),但发现我的“小概率”所涉及的两条基本公式,与“反脆弱”基本一致。 例如,掷一枚公平的六面 骰子,其每次“点数”的期望值是多少?
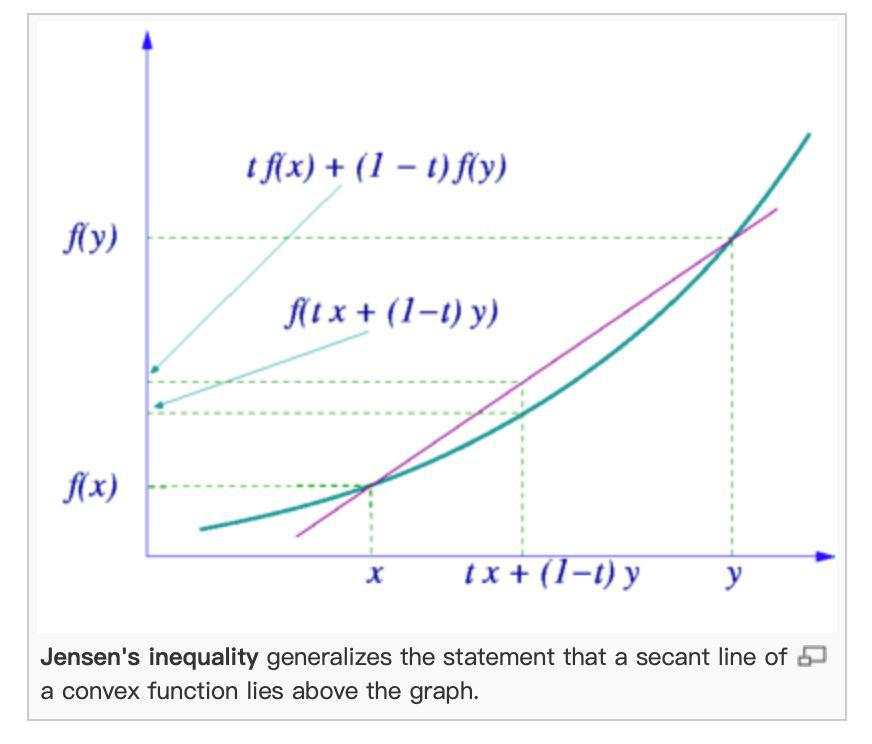
尽管计算如此简单,但是光是这个小数点儿就让人抓狂。所以在上一篇文章为什么真正聪明的人都是概率高手?(零公式入门篇)里我才不厌其烦地用“平行宇宙”来打比方。 但是上一篇文章里没有说的是:每个平行宇宙的胖瘦是不一样的。 为了早点儿结束这一篇文章,我将在下一篇里再说平行宇宙的胖瘦。 另外一个公式是琴生不等式(也称为詹森不等式),它给出积分的凸函数值和凸函数的积分值间的关系。
琴生 不等式是关于凸性(convexity)的不等式。凸性是非常好的性质,在最优化问题里面,线性和非线性不是本质的区别,只有凸性才是。如果最优化的函数是凸的,那么局部最优就意味着全局最优,否则无法推得全局最优。 有很多不等式都可以用琴生 不等式证得,从而可以把它们的本质归结为凸性。 一方面,不管你是押注于大概率事件,还是小概率事件,还是由小概率叠加出来的大概率事件,首先看你要下注于正期望值的事件; 这样一来,你并不需要“准确预测”太多未来,也不惧怕不确定性,随机性和时间都是你的朋友。 没错,投资本质上是一种关于概率的练习。但首先,你必须懂得一些最基本的公式,这样你才能深入至原理层面,而不是懂一堆道理和幻觉。 但是,如果不这样设计,这个炼金术很快就会泛滥成灾,金子就不值钱了。 墨菲定律总在打翻牛奶让人心烦,但时间的方向,人类的意义,全都要仰仗热力学第二定律的坚定和无情。 假如不是如此,我们就无法回答海德格尔在《形而上学导论》中的开篇之问:
“宇宙的历史并不只是由基本定律决定的。它取决于基本定律和除此之外的一长串巧合或者说几率。”
在我看来,如果我们一定要去追寻自己的炼金术,我们要找的,可能就是那些 伪装成小概率的大概率 ,以及 大概率所试图靠拢的基本定律 。
基本理论并不包含那些概率,它们是额外的东西。因此它并不是 万物理论 。 实际上,宇宙中围绕我们的大量信息来自于这些巧合,而不只是基本定律。 现在人们常说,通过检验由低能量到高能量再到更高能量,或者说由小尺度到更小尺度再到更小尺度的现象来逐步向基本定律靠近就像是 剥洋葱 。 我们这么不断继续下去,建更高能的加速器来找寻基本粒子,这样就能够逐步深入粒子的结构,沿着这条路,我们就可以逐渐接近 基本定律 。
我对自己何以在21世纪的这个时间存在于这个世界一直满怀好奇,从物理学和生物学的角度看,生命在地球上繁衍,概率小到不可思议,哪怕是月球的一点微不足道的变化,都会阻止生命最初的出现。
我也感叹斯宾诺莎所说的那位自然之神,其手艺何以这般出神入化、真实可触。 一旦意识到“自我”存在的罕见的小概率,我们就应该继续祈祷这些不可思议的小概率继续发挥作用。 这些小概率,即每个存在于这个世界上的人所依靠所忽视的那些已知条件,地球,太阳,空气,雨水,仿佛被无数条凸性曲线所庇护。 这个世界仅有一盏天平,就是灾难痛苦和邪恶罪行对等的天平,除此之外再无其它,衡量自己幸福的标准不是受过多少享乐,而是躲过多少灾祸。 即使是世俗层面的财富追求,也无法脱离从古至今哲学家们的洞察。 我们需要找到自己的 凸性 曲线(尽管与宇宙已有的凸性曲线对比微不足道),尽情与这个不确定世界的 小概率 共舞。 Reprinted from 微信公众号 ,the copyright all reserved by the original author.
Disclaimer: The content above represents only the views of the author or guest. It does not represent any views or positions of FOLLOWME and does not mean that FOLLOWME agrees with its statement or description, nor does it constitute any investment advice. For all actions taken by visitors based on information provided by the FOLLOWME community, the community does not assume any form of liability unless otherwise expressly promised in writing.
FOLLOWME Trading Community Website:
https://www.followme.com
If you like, reward to support.













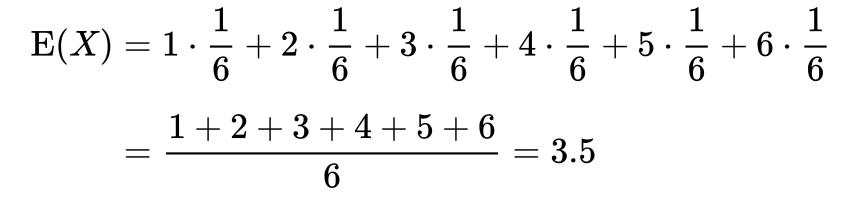



Hot
No comment on record. Start new comment.